Advent of Code, years [y for y in AoC if y%5==0]

It's the end of the year and that also means we have a new Advent of Code, my favourite community event. Each day a new puzzle unlocks - they get harder as the month goes. They have always two parts, you can access the second part after solving the first. It's language agnostic, but I'm rolling with python.

I've been solving these for some time now and I'm building a library to address the most common problems. Highly recommended you do the same - it makes the process so much more enjoyable.

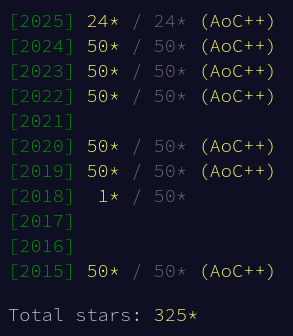
Of course, I'm tackling 2025. I also completed 2015 and 2020 since I wish to solve all of them. Minor spoilers are all over this article, I've tried to hide the major spoilers in footnotes ⁰. There are also a couple of tooling updates. All solutions available in my GitHub repo.

As this is my last article for this year, I wish you all the best for the new year of 2026. May your meetings be short, your bugs findable and all security severities low.

Let's first tackle the current year.

The elves learned about project management, so all that's left to do for us is to decorate 12 rooms in 12 days. It's okay, we promise, no need to worry.

Look, this isn't my first rodeo with the elves, so I was fully expecting a twist along the lines of: “the elves failed to plan properly and you need to fix their screw ups”. It would have been really funny and I was hoping for a full set of puzzles.

This year felt pretty smooth until day 9.

Day 3, day 4 and day 8 I’ve got no notes. Day 1 and day 6 were a bit fiddly. In day 2 and day 5 I was happy to re-use my interval library. In day 7 I was proud to start with the dynamic approach straight away and it went well.

Let's get to the fun parts and spoilers.

In day 9, we have a polygon and we need to find a maximum rectangle that's defined by the vertices of that polygon.

In part 1 you can just check all the pairs, nothing too fancy. I’ve managed to create an off-by-(1,1) error, which I’ve found funny.

In part 2, your need to check if all of the points are within the shape. I am proud to have solved the general problem, even though it's slow ¹.

Day 10 features multiple mysterious buttons and we need to press them a correct amount of times.

I’ve realized that in part one you only need to iterate through subsets of buttons as two presses of one button cancel out.

In part two, I was happy to notice that this is actually a system of linear equations. However, we’re searching for a positive integer solution, which makes this an Integer Linear Programming problem. That's NP-Hard ².

The keyword for day 11 is graph. I hate graphs. We need to find paths in it.

Fortunately, for part 1 a naive approach worked well.

So let's dive into part 2. It's actually a directed acyclic graph. Which means that one of the inner nodes will always be before the other ³.

In the final stretch are tasked with aligning weird shapes to a limited rectangle. That's called a Bin packing problem and it's also NP-hard. I thought there's gotta be a trick to it. And there is ⁴.

This year was very pleasant. The more difficult problems were interesting, they didn't feel unfair nor annoying to me. Seems that Eric really nailed the puzzle design on this one.

I respect the decision to shorten the year and I see the benefits of a more relaxed schedule. In my case, that means more advent of code.

When I’ve realized that I would have time to try some older years, I got excited. I like complete collections and I want a full set of solutions for all AoC years. Naturally, I wanted to start from the beginning, in this case 2015.

I had no issues in the first 14 days whatsoever. I thought it was quite funny to brute force some MD5 hashes on day 4. There was also some unescaping on day 8 and JSON parsing on day 12. I found these puzzles quite practical as opposed to abstract/academic.

As always, I had to make an effort to solve dynamic programming/memoization puzzles. Day 15 was a nice warmup. On day 17 it was surely possible to use it, but I just checked all subsets.

I was happy to stretch my math muscles on day 20. In the end, the solution is kind of dumb ⁵. Another "math" day was day 25, where I immediately recognized the integer - rational number bijection and a finite field to iterate through.

I struggled quite a lot on day 19, part 2. General case is very tough, so you’d better analyze your input well ⁶.

Day 21 was tough and day 22 was tougher. So many rules to track, my solution barely works. And I would love to drop some hints or spoliers, but I am afraid I can't - these are all about the execution, the plan is clear.

First of all, huge kudos to Eric that the first year is still available and fully functional. No breaking changes in 11 years is an achievement - it also means he nailed the mechanics in one shot.

I liked the more practical focus on real-world algorithms and schemas. I also liked the sense of humor in the assignments - Aunt Sue from day 16 being my favorite. An overarching story wasn't there the first year, but that was fixed soon.

The year is still not over. I am hungry for more. If I want to finish another one this year, I have to be fast and precise.

Look at me go - taking a relaxing and fun event and turning the pressure up for no reason. I don't know why am I like this. Anyway!

The internet agreed that year 2020 is one of the more pleasant years. It also makes for a nice pattern of selected years (see the title).

After 2020, we are heading for a vacation. And what a year it was, I remember the Covid pandemic quite well. With hindsight, it's easy to think it was overblown. At the time though, we didn't know what the long term effects were. Anyway, we all were looking for a break at the end of the year.

So if all else fails, let's pretend we're travelling to some remote tropical islands.

There are some patterns that repeat. Wrangling data into lists and dataclasses. Interpreters of small instruction sets (day 8, day 12, day 24). The game of life (day 11, day 17, day 24). Validating strings against arcane rules (day 2, day 4, day 16). Weirdly defined sequences (day 9, day 15, day 23, day 25).

What I mean is the more problems you see, the better you're equipped to deal with them. It's not that big of a shock, because you already have a couple of tricks in the bag to try out.

And yet some days surprise me. On day 18 we’re evaluating expressions with a different order of preference between addition and multiplication. I know that I should build a tree. But it was a while since I did it. Looking for general hints I’ve discovered a two stack algorithm. Guess I need to do a recap of data structures - those come in handy on day 23 as well ⁷.

Another tension in these problems is between trying to solve the general solution (because you anticipate the issues that will come) and looking at the particular input for shortcuts. I still prefer a general solution, but there is an art to ignoring the hard parts of a problem and getting away with it.

In day 19, I’ve successfully shortcut the general solution. In day 20 I’ve done so for part 1 (as we're only interested in corners) and to a lesser extent part 2 ⁸. Nevertheless, day 20 part 2 is the messiest code I’ve written in a long time, but it delivers. And hey, finally a nice visualization I can share.

Some problems this year were quite scary and the general cases might have been unpleasant. Fortunately, the actual inputs weren't so difficult, so plenty of shortcuts could be had. With the exception of day 20, they weren't tedious, which is great.

Not going to lie, doing three sets of problems instead of one takes a toll. I am quite done for this year, it is time to rest. I couldn't have done it without my prepared library.

As the latest year has only 12 days, I had to modify the logic of day validation. Nothing too bad, small generalization.

I also had a slight issue in the tests as some substrings I use over and over trigger vim modelines. So I've added # vim: nomodeline to each test and to the test template as I'm not using those at all.

I wanted to add caching logic for the submitted wrong solutions (to remember if a wrong answer was already sent, maybe parse the response to know if the answer needs to be higher/lower). But I didn't do it, so maybe next year.

In the stdlib I've added couple simple methods to map2d (yes, all done for 2020, day 20 part 2):

• Flipping and rotating maps, always returns a new instance,
• Joining maps to new instances,
• Getting borders of the map and trimming them away.

Finally I've implemented small set of methods for prime numbers, factorization, sieve of Eratosthenes, EGCD, modular inverse and Chinese Remainder Theorem. Wrapped up in a single "num theory" module.

Last (and probably least as well) I've started using black everywhere just to be consistent.

Three sets of advent of code puzzles can be done in a single month. I'll attempt to do the same next year, maybe I'll start a bit sooner so that the schedule is more relaxed. I will have the complete collection one day.

There are two bigger points I'd like to write-up some day.

One is about the distinction between problems and exercises and the approaches to address each. When I was a child I was doing some competitive math. I wasn't the greatest at it, but I've learned a few tricks. These were all problems. Difficult, time-consuming, unclear, sometimes ill-defined. Contrasting with exercises which are straightforward (not necessarily easy).

The other is to dive deeper into SAT solvers. Going back to the P vs NP question to see how the mad geniuses try and shortcut these difficult issues. I've used Z3 nearly every year and I am quite convinced it's actually black magic.

But that can be done on some other day. Enjoy the rest of the holidays - Christmas might be over and I don't know about you, but we're still munching on the seasonal cookies. Once again, I wish you all the best for the new year of 2026. Hope you're successful in all your efforts and with good health and happiness thorough the year.